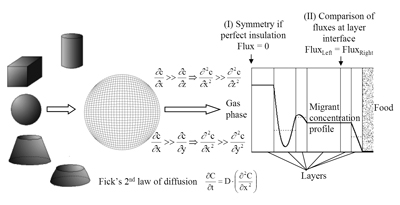
图1. 基于五种基本几何形状的建模示意图。所有食品包装被简化为序列单层的分析。

如今，计算机模拟技术已经可用于预测食品塑料包装物中的添加剂至食品中的迁移率，然而，目前的模拟软件大部分只能实现对等温条件下单层塑料包装的模拟。本文报道了一种可用来模拟计算多层塑料包装，及在非等温条件下添加剂迁移率的扩散模型，本模型运用有限元分析法（FEA）来解非等温条件下的多层扩散方程。

近年来，已有多种概念及数学工具问世用以模拟包装材料至食品中的迁移问题，基于这些工具的用户友好型软件也已经开始进入应用领域，并已被欧盟及瑞士立法机构认定为法定工具。然而，此种扩散模型仅限于单层包装在等温条件下的扩散问题。而涉及到多层包装体系及真实的非等温储存条件时，此种模型则显得无能为力。

本研究的工作针对目前的模拟程序做进一步的发展, 开发了一种基于有限元分析（Finite Element Analysis-FEA）原理的软件，以解决在非稳态的实验条件下，对多层包装结构中物质迁移的模拟问题。

#p#

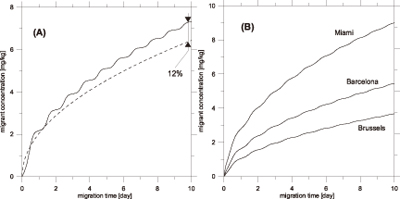
图2. 温度变化对添加剂迁移率的影响，（A）实线为正弦温度变化条件下，虚线为等温条件下；（B）为不同城市气候下的模拟数据对比。

多层包装的扩散及迁移建模

本文中多层体系中各层中的浓度分布曲线由FEA法计算得出。

模型总体描述

基于以下假定建立简单有效的模型：（1） 迁移只受扩散过程支配（Fick's law），而不考虑其他动力学步骤；（2）迁移物在各层包装及食品中的平衡浓度分别由物质在各层间及食品与包装中的分配系数K决定；（3）食品与包装表面紧密接触（无空隙）；（4）迁移物在包装-食品界面的迁移迅速且在食品中分布均一；（5）迁移物在包装-空气界面的迁移为0。

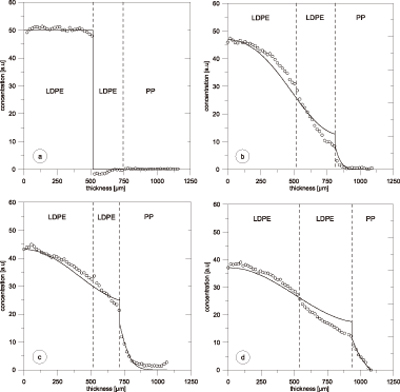
图3. LDPE/LDPE/PP复合膜中添加剂迁移浓度分布曲线的实测值及模拟值。扩散时间为：0min （a），51min（b），84min（c），154min（d）。实线为模拟曲线，点线为实测曲线。

#p#

食品包装层的形状基于预定的五种几何体：矩形、圆柱体、球形、切尖圆锥、球缺。如果食品包装的具体几何形状不在以上几种范围内，可用体积比表面来定义（S/V），如图1所示。

变温条件下的包装添加剂迁移率模拟

时间相关扩散系数的优点在于可以在各种环境温度情况下预测包装物迁移及比较扩散效果。这对精确模拟真实条件下经历不同温度环境下，如加工、包装、储存及消费者最终加工过程（食品在包装中加热）中的包装物材料迁移极为有价值。对于每次温度变化，程序重新计算新的迁移物扩散系数。因此，在各种温度条件下，如阶梯变化、震荡、温度冲击，乃至真实气候条件下，都可以对包装物中添加剂的迁移进行模拟。

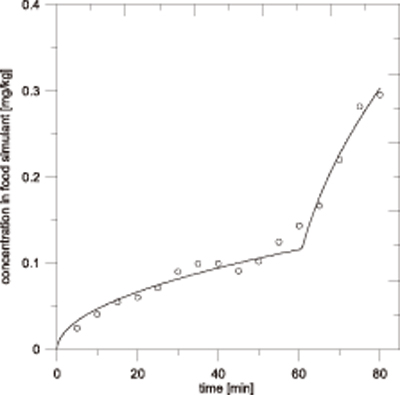
图4. 阶梯升温状态下HP136至己烷中的迁移浓度曲线，25℃等温60min，然后60℃等温20min。实线为模拟曲线，点线为实测曲线。

我们对250μm 厚的高密度PE膜中的添加剂扩散情况进行了模拟，其中含1000ppm添加剂（摩尔质量350 g/mol）。迁移曲线结果示于图2A。尽管两例中平均温度均为20℃，但得到的迁移曲线结果却明显不同。与等温状态相比，温度震荡条件下的扩散系数呈波状周期变化且添加剂迁移量显著增加。等温模拟条件下，食品中添加剂最终迁移浓度结果偏低12%。对比结果明确显示了忽略温度变化的迁移率模拟会导致背离真实值的较大偏差。通过在程序中设定气候变化条件，可以预测在各种真实气候下的添加剂迁移结果。图2B所示为假定将相同包装的食品在11月于世界不同城市室外储存10天的迁移结果。

#p#

对模拟计算结果的验证

数学验证

计算精度可由边界条件验证，并与从法定程序得到的结果作为真实值进行对比。1200次试验的相对误差，呈正态分布，且有95%的位于+/- 1.21%间。另外，95%的相对误差为负误差，说明数学模拟的结果略高于真实值，因此对于风险评估而言通常会产生可靠的结果。由此可见，此种数学模拟产生的结果精确可靠。

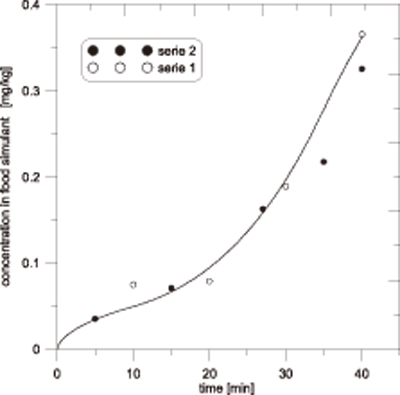
图5. 线性升温状态下HP136至己烷中的迁移浓度曲线。实线为模拟曲线，点线为实测曲线。

#p#

试验验证

本文通过自制的简单多层聚合物材料进行实验，以简化添加剂迁移量的测量实验过程。

样品制备与迁移实验

PP及PE膜由粒料用P 200 T热压机压制而成，多层膜由各单层膜在低温下压制而成。实验温度下含饱和二苯甲酮的添加剂层由样品薄膜在较高温度下（70~80℃）于添加剂中浸泡制得，二苯甲酮在LDPE中达到饱和浓度（4.5% at 70℃）。含5% HP 136?的添加剂层通过将HP 136?置于两层PE膜间压制而成。

所有的模拟计算通过独立研发的软件“SML”进行。模拟计算中LDPE及PP中的添加剂扩散系数由独立实验得到。

多层聚合物膜中的扩散行为

图3所示为在PE-PE-PP 结构样品中4次不同扩散时间后的实验结果。浓度分布曲线由实验所得的扩散系数计算而得（在 PE 及 PP中，D=1.3×10-7 cm2/s，及 8.53×10-9 cm2/s），并且通过优化分配系数KPE/PP 以得到与试验结果的最优匹配。由分配系数（KPE/PP = 1.5）引起的 PP-PE界面的浓度突变，及由二苯甲酮慢速扩散引起的PP层中浓度分布曲线的巨大斜率， 都得到了正确的模拟。

聚合物体系中的非等温迁移

样品池置于GC炉中，通过控制实验中的温度，每隔一段时间采集一定量的样品进行GC进行分析。

简单温度变化条件下，迁移率的软件模拟值与实验值的结果对比示于 图4 及图5。图4中，样品由25℃快速阶梯升温至60℃。图5中，样品从30℃以1℃/min 连续升温至70℃/min 。

两图都显示了软件模拟结果与试验结果的高度符合。由此可见，FEA模型可以模拟迁移过程中扩散系数非恒定的实验条件且Fick's扩散模型在此种条件下完全适用。

以上实验说明，即使短时间内较小的温度变化也会导致较大的添加剂迁移率变化。因此，模拟分析软件必须考虑温度变化的影响因素。

结论

本研究展示了将FEA法用于迁移率模拟计算的可能性及优势，可以精确计算在真实温度条件下添加剂由多层聚合物包装至食品中的迁移情况。我们将进一步测试程序以证明本方法不仅适用于 的模拟样品，并且适用于真实的食品包装。从技术角度看，数学模拟方法具备足够的潜力及灵活性以满足大多数潜在用户的需求（如小体积包装，食品引起的溶胀效应，与食品间的迁移反应，材料中的温度梯度等）。如今，添加剂在聚合物中扩散系数的数据库日趋完善，并可运用于模拟软件中。待分配系数等各种必需参数逐步完善后， 添加剂迁移模拟软件的发展必将更进一步，为食品包装安全的预测工作带来革命。